JS 관련 밈을 보면 JS가 어처구니 없는 결과 값을 보여주는 순간들이 있어서 웃긴 것들이 꽤 있는데,
그 중에 1.1+1.2 == 2.3 이 false라는 것도 심심찮게 보이곤 한다.
그걸 보다가 왜 저런 결과가 나오는건지 궁금해져서 조금 찾아보게 됐는데, 이는 비단 JS 만의 문제가 아니라
float, double 형을 쓰는 모든 언어들이 같은 문제를 겪는다고 볼 수 있다.
오늘은 이 이야기를 해보고자 한다.
컴퓨터는 기본적으로 이진법 즉, 0과 1로 모든 말을 알아듣는다. 당연히 실수를 저장할 때도 10진수로 표현된 수를 이진법으로 변환해서 저장을 할텐데, 이 때 소수점 아래 내용을 저장하는 방식이 여러가지로 쓰인다.
여기서는 일단 float, double형에서 사용하게 되는 부동소수점 방식을 다룰건데, 생각보다 그리 어렵지 않다.
(IEEE 754 프로토콜 기준으로)
일단 우리가 흔히 알고 있는 0.1, 0.125 이렇게 .의 위치를 고정시켜 명시함으로써 이 아래가 소수의 영역이다 라고 이야기를 하는 것을 우리는 고정소수점이라고 부른다. 하지만 이 방식의 경우 부동소수점 방식 보단 더 넓은 범위의 수를 표현할 수가 없어 컴퓨터는 부동소수점 방식을 주로 사용하고 있다.
그럼 부동소수점 방식이란 무엇인가?
설명이 어려운데, 소수점의 위치를 따로 명시하지 않고, 소수점의 위치가 어디다 라는 숫자 값을 정해두는게 부동소수점 방식이라고 할 수 있다.
대충 입력이 되는 방식은
우선 저장하고 싶은 수의 부호를 먼저 정해두고, 해당 수의 절댓값을 이진수로 변환한다. 그리고 소수점의 위치를 왼쪽에(그러니까 정수부에) 1하나만 남을때까지 옮기고, 옮긴 횟수는 2의 n(옮긴 횟수) 제곱으로 표시해준 다음 저장하는 방식인거다.
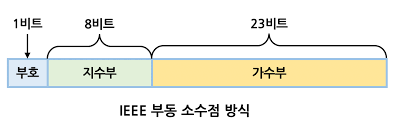
여기서 그림의 지수부 가수부를 확인할 수 있는데 소숫점을 기준으로 왼쪽 * 2의 n제곱 은 지수부로 저장, 오른쪽은 가수부로 저장한다고 생각하면 될 것 같다.
가수부의 영역보다 수가 모자라다면 남는 자리는 모두 0으로 채워준다.
ex)
1. +-
2. 11110111.111 이라고 가정하면 1.1110111111 로 만들어주는데 점을 왼쪽으로 7번 옮겼으니까 2의 7제곱을 해줘야함.
3. 결과를 표시하면 2^7 * 1 이 지수부, 1110111111 여기가 가수부가 된다고 생각하면 되겠다.
하여튼 이렇게 저장하는게 부동소수점 방식인데, 여기서 이제 문제가 발생한다.
10진수를 2진수로 변환했을 때 딱 32비트 공간안에 떨어지도록 만들어지면 참 좋겠지만 오차라는게 있다. 예를 들어 0.125와 같은 숫자는 그 공간에 들어가기 때문에 아무런 문제가 없지만 그냥 0.1 이런 애들은 소수점 아래가 길게 이어지는 원주율처럼 2진법이 길게 이어진다. 그럼 정해진 공간안에 저장되어야하는 조건 상 딱 사이즈 맞는 만큼만 넣어두고 나머지 뒤의 수들은 자르게 되는데, 여기서 오차가 발생하는거임..
이게 하나만 있으면 얼마 안되는 차이가 되겠지만, 두개, 세개, 열개 이렇게 모이면 꽤 큰 차이를 보이기 때문에 오차가 꽤 생긴다고 볼 수 있다.
이런 이유로 우리가 1.1 + 1.2 == 2.3 이 false인 상황을 볼 수 있게 된다.
아 추가로 float와 double의 차이는 32비트, 64비트 저장공간 그 차이다.
double로 쓰면 당연히 float보단 오차가 좀 줄어들겠지만, 그래도 수가 커지면 이것도 오차가 생길 것..
'Dev > JavaScript' 카테고리의 다른 글
| [TypeScript] TypeScript (0) | 2023.06.02 |
|---|---|
| [JavaScript] 함수는 1급 객체 (First-Class Object) (0) | 2023.06.01 |
| [JavaScript] parseInt() (0) | 2023.05.23 |
| [JavaScript] Hoisting (0) | 2023.04.20 |
| [JavaScript] Scope & Closure (0) | 2023.04.20 |